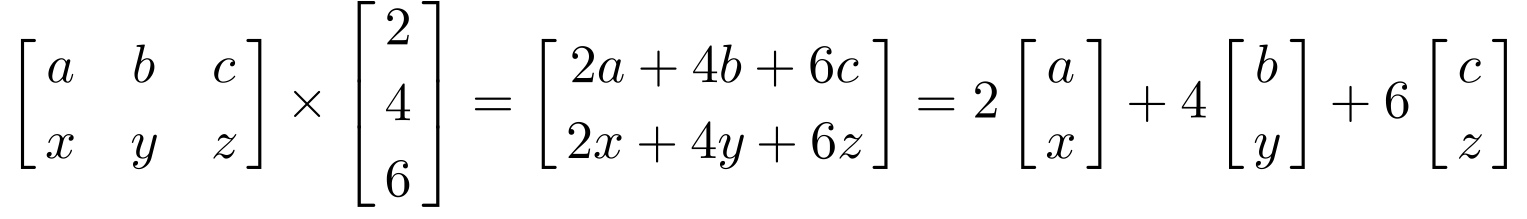Why Does Matrix Multiplication Work the Way it Does?
One problem I often struggled with when being introduced to new concepts in mathematics, is that a lot of the mechanics of how you do something looks completely arbitrary.
One of these cases are matrix multiplications. The result depends on the sequence matrices are multiplied. Here are some examples.
Row × Column
If we multiply a 1x3 row vector with a 3x1 column vector we get a scalar as result.
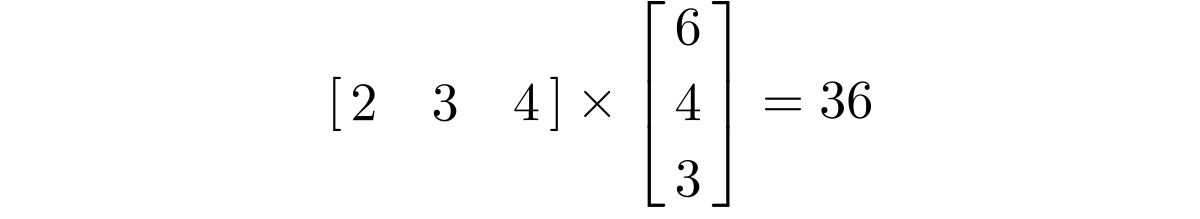
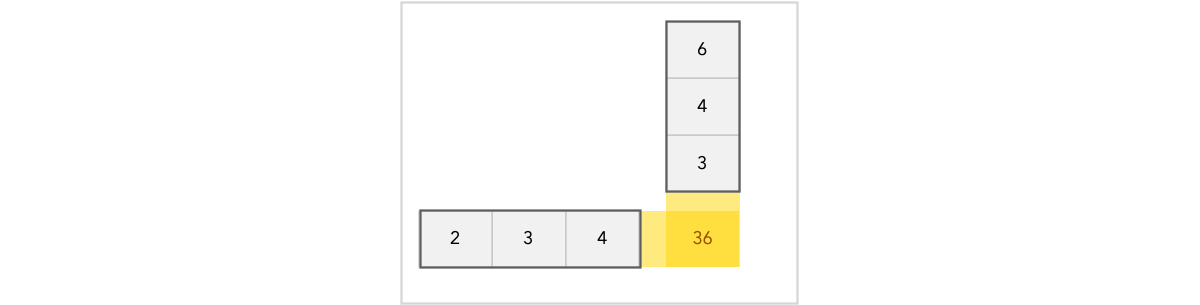
Below is an illustration of how it works. We do a dot product of the row with the column. Matrix multiplication is really just a compact way of representing a series of vectors you want to combine with a dot product. The pattern will become clearer with the next examples.
Column × Row
However if multiply a 3x1 column vector with a 1x3 row vector we get a 3x3 matrix as result.
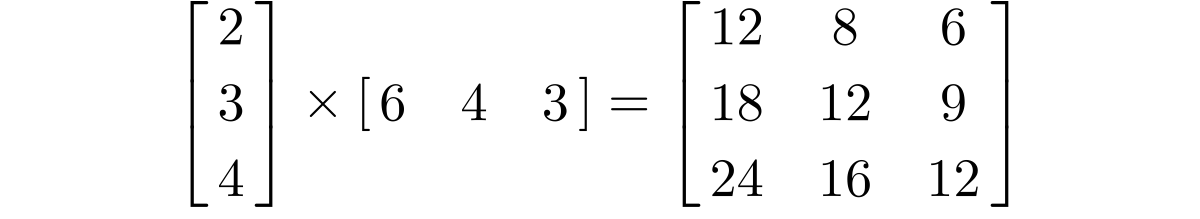
Below is a visual explanation of how matrix multiplication works.
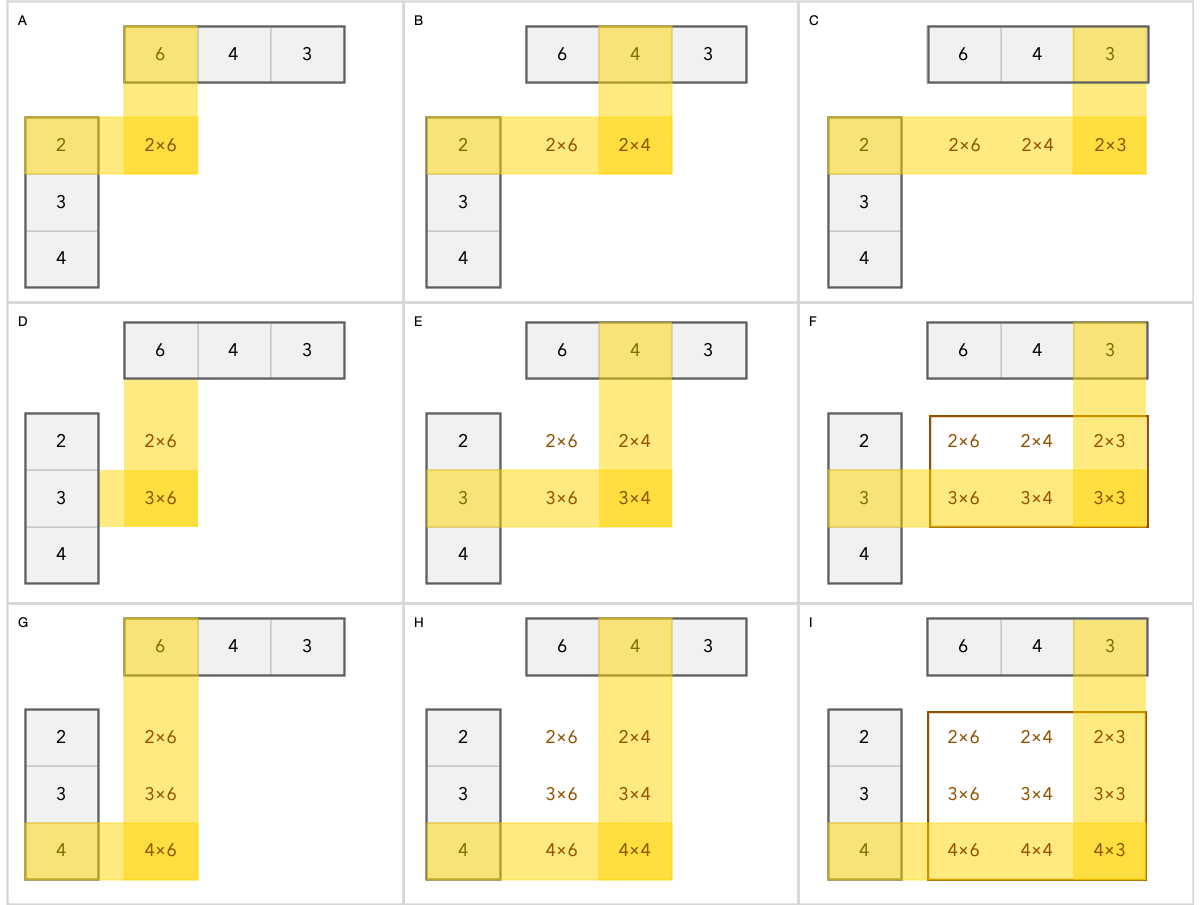
You can see that every cell in the new matrix is made up of a unique combination of rows from the first vector and columns in the second vector being multiplied.
It also should give the first clue to why you cannot multiply columns with columns or rows with rows. If you did there would be no system of determining the row and column index of each new element calculated.
The way matrix multiplications are setup, every resulting element get their row position from the first argument, and their column position from the second argument.
Let us explore this by multiplying actual matrices and not just vectors.
Matrix × Matrix
Below is an example of multiplying two matrices. We got a 2x3 matrix (two rows and three columns) multiplied by a 3x2 matrix producing a 2x2 matrix.
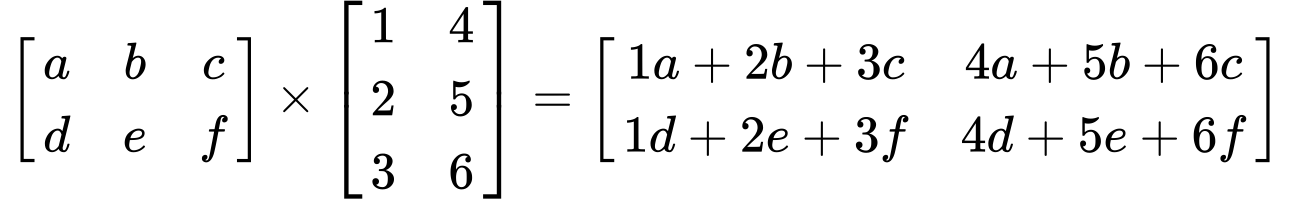
Let us illustrate the process graphically. As you can see, the resulting matrix has to be 2x2. Why? Because every element is determined by the rows in the first matrix and columns in the second matrix.
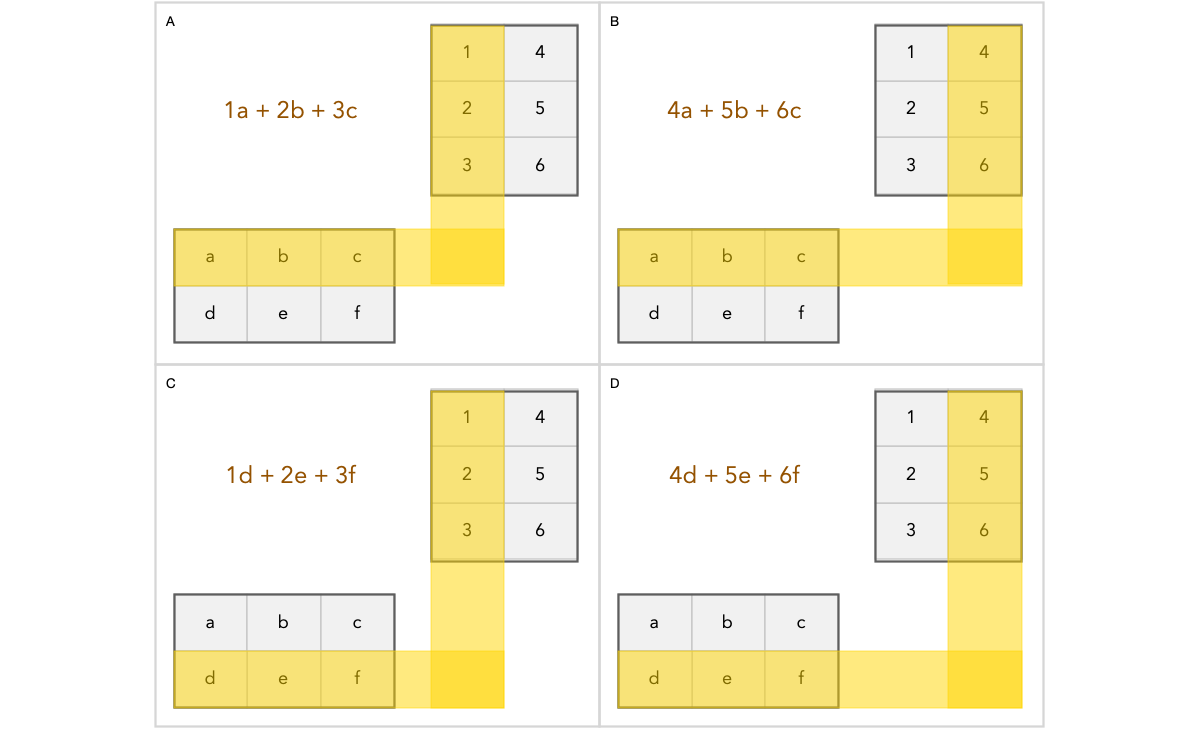
It may seem random how matrix multiplication is defined. Why does the second matrix have to be oriented completely different from the first matrix to make the multiplication happen?
The problem with having both matrices oriented the same way is that then we would have no system for determining which cell in the result matrix we should store the result of performing the dot product of two vectors.
Rules to Remember About Matrix Multiplication
This are just simple rules to help you remember how to do the calculations.
- Rows come first, so first matrix provides row numbers. Columns come second, so second matrix provide column numbers.
- Matrix multiplication is really just a way of organizing vectors we want to find the dot product of.
Looking at Matrix Multiplication as a Linear Combination
This is a slightly different way of thinking about matrix multiplication.
If you have the vectors:
v₁, v₂, ..., vₙAnd scalars, which we will refer to as weights.
c₁, c₂, ..., cₙThen y is called a linear combination of said vectors:
y = c₁v₁ + c₂v₂ + ..., cₙvₙWe can use matrices to express this in a compact form. Let us consider an example where the vectors are:
[a, x], [b, y], [c, z]Please note that we are actually writing column vectors here. If these had been row vectors, we would have written [a x] instead.
And the weights are:
2, 4, 6Then we can combine the column vectors into a matrix and multiply it by a column vector representing the weights.